Man, the 19 times table. It’s the absolute worst. Every multiplication table up to 12 is fine. Maybe 13 and 17 get a little messy. But 19? That sucker is designed to make you feel stupid. For years, I just swallowed it, relying on calculators or that old trick where you multiply by 20 and subtract the extra—but honestly, that’s just more steps, and when you’re trying to think fast, those extra steps are where you mess up.

I didn’t set out to conquer the 19s. I really didn’t. This whole thing started because my nephew, Leo, was having a complete meltdown. He’s in that phase where they expect him to know all these tables instantly, and he kept freezing up on 19. I told him, “Look, kid, every hard math problem has a cheat code. I’m going to find it, document it, and we are going to nail this.”
My Initial Practice: The Brutal Grind
My first step, which was stupid, was just trying to memorize it again like I was seven. I got through 19 x 5 fine, maybe even 19 x 6. But by the time I hit 19 x 8, my brain was mush. My log looked like this:
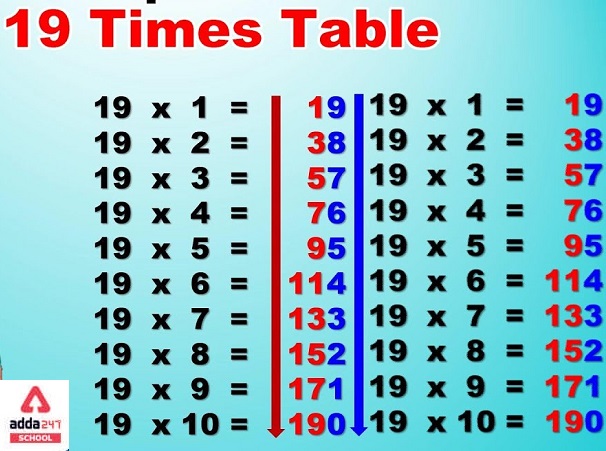
- 19 x 1 = 19 (Easy)
- 19 x 2 = 38 (Okay)
- 19 x 3 = 57 (Getting warmer)
- 19 x 4 = 76 (Wait, 76? Why isn’t it 77?)
- 19 x 5 = 95 (Fine)
- 19 x 6 = 114 (Ugh, I need to borrow the 1, that just complicated the mental jump)
I realized brute force wasn’t going to work. Leo needed a pattern he could see instantly, something that didn’t require him to remember a complicated set of rules or perform long subtraction (the 20-N method). I threw out everything I thought I knew and started looking at the sequence itself.
Unlocking the Pattern: The “Add Two, Minus One” Method
This is where the actual practice log gets interesting. I decided to stop thinking about 19 as a whole number and start thinking about how the digits shift. I took a piece of paper and just focused on the tens column and the ones column, ignoring everything else.
I asked myself: How does the tens digit change? How does the units digit change?

The magic is this: As you move down the 19 table, the tens column always increases by 2, and the units column always decreases by 1.
I started testing this theory out, recording the digits as I went:
- 19 x 1: Tens starts at 1. Units starts at 9.
- 19 x 2: I apply the rule: 1 + 2 = 3. 9 – 1 = 8. Result: 38. (Checks out!)
- 19 x 3: Next starting point is 3/8. Apply the rule: 3 + 2 = 5. 8 – 1 = 7. Result: 57. (Checks out!)
- 19 x 4: Next starting point is 5/7. Apply the rule: 5 + 2 = 7. 7 – 1 = 6. Result: 76. (Checks out!)
- 19 x 5: Next starting point is 7/6. Apply the rule: 7 + 2 = 9. 6 – 1 = 5. Result: 95. (Checks out!)
This was it! This was the cheat code. The beauty is that the units column perfectly counts down from 9 to 0, which makes it super easy to track. If Leo knew he was multiplying by 7, he knew the answer had to end in 3 (9 -> 8 -> 7 -> 6 -> 5 -> 4 -> 3).
Turning Practice into Instant Recall
The practice shifted from memorizing answers to memorizing the count-down sequence (9, 8, 7, 6, 5, 4, 3, 2, 1, 0) and pairing it with the sequential odd numbers in the tens column (1, 3, 5, 7, 9, 11, 13, 15, 17, 19). It was effortless compared to traditional methods.
I used flashcards, but instead of writing the answer, I wrote the two rules: Tens (+2), Units (-1). Within two hours, Leo was flying through the tables. He was laughing, actually laughing, because he felt like he had cheated the system.
Why Did I Care So Much About a Kid’s Math Test?
It seems ridiculous, right? A grown man spending a weekend obsessed with the nineteen times table. Why the intensity?
The real reason I got so focused on this was a comment my boss, old miserable Frank, made last month. We were sitting in a planning meeting, discussing some budgeting figures. It was nothing major, just rounding off costs for five different projects. Frank looked at me and said, loud enough for the whole room to hear, “Just use the calculator, Steve. We all know mental arithmetic isn’t your strong suit. Remember that time you messed up the catering order totals?”
I was furious. It was completely unprofessional, and frankly, embarrassing. I kept my cool in the meeting, but later that day, I promised myself I would eliminate every single tiny weakness Frank might ever try to weaponize again. I decided I wasn’t going to just be “good enough” at quick math; I was going to be flawless. I pulled up online tests for basic arithmetic, algebra, anything that required fast thinking. The 19 times table was one of the first things that cropped up on a speed challenge, and I flubbed it.
So, Leo’s problem became my immediate, personal vendetta against Frank’s insulting remark. I didn’t just find the trick for Leo; I drilled it into myself until I could answer any 19x question faster than Frank could pull his greasy phone out of his pocket.
A week later, we were in a similar meeting, discussing logistics. Frank started to pull out his calculator to multiply a complex number by 19. Before he could even unlock the screen, I just threw the answer out there. Perfect. He squinted at me, looked at his calculator, and didn’t say a word. He didn’t mock me again.

That feeling of proving him wrong, simply by mastering this ridiculous pattern, was priceless. That’s why I documented it. This isn’t just a math hack; it’s proof that you can take any seemingly difficult task, break it down, find the inherent pattern, and beat it instantly.
Try it. Next time you’re stuck on 19 x 7, just remember: it ends in 3 (9-8-7-6-5-4-3). The tens digit is the 7th odd number (1, 3, 5, 7, 9, 11, 13). Boom: 133. Instantaneously unlocked.
